联合熵、条件熵、散度与互信息

联合熵（Joint Entropy）

对于两个离散随机变量 $X$ 和 $Y$，其联合熵定义为：

$$\begin{array}{r}H(X,Y)=-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(x,y)\end{array}$$

其中 $P(x,y)$ 为 $X$ 和 $Y$ 的联合概率密度函数。

上述公式的计算是通过将 $X$ 和 $Y$ 的所有可能取值组成的信息熵的期望值。

条件熵（Conditional Entropy）

对于离散随机变量 $X$ 和 $Y$，其条件熵定义为：

$$\begin{array}{r}H(Y\mid X)=-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(y\mid x)\end{array}$$

其中 $P(y\mid x)$ 为 $Y$ 在给定 $X$ 的情况下的概率密度函数。

考虑是随机变量，因此有 Naive Bayes：

$$\begin{array}{rl}P(y\mid x)& =\frac{P(x,y)}{P(x)}\\ P(x)P(y\mid x)& =P(x,y)\end{array}$$

$$\begin{array}{rl}H(Y\mid X)& \equiv \sum _{x\in {\mathcal{R}}_X}P(x)H(Y\mid X=x_i)\\ & =-\sum _{x\in {\mathcal{R}}_X}P(x)\sum _{y\in {\mathcal{R}}_Y}P(y\mid x)\log P(y\mid x)\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x)P(y\mid x)\log P(y\mid x)\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(y\mid x)\\ & =-\mathbb{E}[\log P(Y\mid X)]\end{array}$$

如果做更多改写，则有：

$$\begin{array}{rl}H(Y\mid X)& \equiv \sum _{x\in {\mathcal{R}}_X}P(x)H(Y\mid X=x_i)\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(y\mid x)\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log \frac{P(x,y)}{P(x)}\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)[\log P(x,y)-\log P(x)]\\ & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(x,y)+\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(x)\\ \because & \sum _{y\in {\mathcal{R}}_Y}P(x,y)=P(x)\\ \therefore & =-\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log P(x,y)+\sum _{x\in {\mathcal{R}}_X}P(x)\log P(x)\\ & \\ & =H(X,Y)-H(X)\end{array}$$

因此我们可以得出

$$\begin{array}{rl}H(Y\mid X)& =H(X,Y)-H(X)\\ H(X\mid Y)& =H(X,Y)-H(Y)\end{array}$$

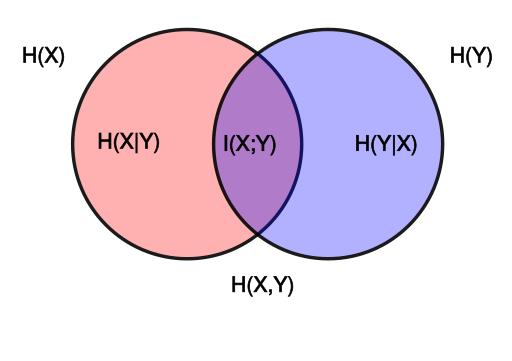
通过类似运算，我们可以获得如下韦恩图：

[https://commons.wikimedia.org/w/index.php?curid=11245361]

相对熵（Relative Entropy）

相对熵又叫 KL 散度，是衡量两个概率分布之间的差异性（或者说距离）。

我们假定两个相对于离散随机变量 $X$ 的概率分布 $P(x)$, $Q(x)$。对于这两个概率分布，每一个概率都有 ${\sum }_{x\in {\mathcal{R}}_X}P(x)=1$ 和 ${\sum }_{x\in {\mathcal{R}}_X}Q(x)=1$，且 $P(x)>0$ 和 $Q(x)>0$。

其相对熵定义为：

$$\begin{array}{rl}{D}_{\text{KL}}(P\parallel Q)& =\sum _{x\in {\mathcal{R}}_X}P(x)\log \frac{P(x)}{Q(x)}\\ & =\mathbb{E}\left[\log \frac{P(x)}{Q(x)}\right]\end{array}$$

考虑是对两个概率比值的期望值，因此有： $$D_{\text{KL}}\ge 0$$

当且仅当两个概率密度相等时，相对熵为 0。

$$\begin{array}{rl}{D}_{\text{KL}}& =\mathbb{E}\left[\log \frac{P(x)}{Q(x)}\right]\\ & =\mathbb{E}\left[\log \frac{P(x)}{P(x)}\right]\\ & =\mathbb{E}\left[\log 1\right]\\ & =0\end{array}$$

需要注意的是由于过程中是 $P(x)$ 和 $Q(x)$ 的比值，且存在 $\log$ 函数，因此相对熵不是对称的。即

$$D_{\text{KL}}(P\parallel Q)\ne D_{\text{KL}}(Q\parallel P)$$

而为了解决不对称的问题，我们可以使用 JSD 散度： $$\begin{array}{rl}{D}_{\text{JSD}}(P\parallel Q)& =\frac{1}{2}{D}_{\text{KL}}(P\parallel M)+\frac{1}{2}{D}_{\text{KL}}(Q\parallel M)\\ & =\frac{1}{2}\sum _{x\in {\mathcal{R}}_X}P(x)\log \frac{P(x)}{M(x)}+\frac{1}{2}\sum _{x\in {\mathcal{R}}_X}Q(x)\log \frac{Q(x)}{M(x)}\end{array}$$

其中 $M(x)=\frac{P(x)+Q(x)}{2}$。这一节将不会详细讨论 JSD 散度。

互信息（Mutual Information）

对于随机变量 $X$ 和 $Y$，其互信息定义为：

$$I(X;Y)=\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log \frac{P(x,y)}{P(x)P(y)}$$

考虑 KL 散度的定义：

$$\begin{array}{rl}{D}_{\text{KL}}(P\parallel Q)& =\sum _{x\in {\mathcal{R}}_X}P(x)\log \frac{P(x)}{Q(x)}\end{array}$$

如果我们将 $P(x)$ 替换为 $P(X,Y)$，$Q(x)$ 替换为 $P(X)P(Y)$ 则有：

$$\begin{array}{rl}& D_{\text{KL}}(P(X,Y)\parallel P(X)P(Y))\\ =& \sum _{x\in {\mathcal{R}}_X}P(X,Y)\log \frac{P(X,Y)}{P(X)P(Y)}\\ =& I(X;Y)\end{array}$$

因此我们可以认为互信息是 $P(X)P(Y)$ 和 $P(X,Y)$ 之间的距离。因此如果 $X$ 和 $Y$ 相互独立，$P(X)P(Y)=P(X,Y)$，则互信息为 0。即：

$$I(X;Y)=D_{\text{KL}}(P(X,Y)\parallel P(X)P(Y))=0$$

互信息也可以通过条件熵来表示：

考虑 Naive Bayes：

$$\begin{array}{r}P(X\mid Y)=\frac{P(X,Y)}{P(Y)}\end{array}$$

$$\begin{array}{rl}I(X;Y)& =\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log \frac{P(x,y)}{P(x)P(y)}\\ \because & P(x,y)=P(x\mid y)P(y)\\ \therefore & =\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log \frac{P(x\mid y)P(y)}{P(x)P(y)}\\ & =\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(x,y)\log \frac{P(x\mid y)}{P(x)}\\ & =\sum _{x\in {\mathcal{R}}_X}\sum _{y\in {\mathcal{R}}_Y}P(y)P(x\mid y)\log \frac{P(x\mid y)}{P(x)}\\ & =\sum _{y\in {\mathcal{R}}_Y}P(y)\sum _{x\in {\mathcal{R}}_X}P(x\mid y)\log \frac{P(x\mid y)}{P(x)}\\ & =\sum _{y\in {\mathcal{R}}_Y}P(y)D_{\text{KL}}(P(X\mid Y)\parallel P(X))\\ & ={\mathbb{E}}_Y\left\{D_{\text{KL}}(P(X\mid Y)\parallel P(X))\right\}\end{array}$$

因此我们获得了

$$I(X;Y)={\mathbb{E}}_Y\left\{D_{\text{KL}}(P(X\mid Y)\parallel P(X))\right\}$$

因此我们可以通过多种方式表达互信息：

$$\begin{array}{rl}I(X;Y)& =H(X)-H(X\mid Y)\\ & =H(Y)-H(Y\mid X)\\ & =H(X)+H(Y)-H(X,Y)\\ & =H(X,Y)-H(X\mid Y)-H(Y\mid X)\\ & ={\mathbb{E}}_Y\left\{D_{\text{KL}}(P(X\mid Y)\parallel P(X))\right\}\end{array}$$

[https://commons.wikimedia.org/w/index.php?curid=11245361]

互信息的一些性质包括：

• 非负性：$I(X;Y)\ge 0$
• 对称性：$I(X;Y)=I(Y;X)$
• 衡量依赖于 $X$ 和 $Y$
  • 当且仅当 $X$ 和 $Y$ 相互独立（记为 $X\perp Y$），$I(X;Y)=0$
  • $I(X;Y)$ 不仅随 $X$ 和 $Y$ 的依赖性而增加，而且随 $H(X)$ 和 $H(Y)$ 的依赖性而增加
• $I(X;X)=H(X)-H(X\mid X)=0$