支持向量机 Support Vector Machine

支持向量机（Support Vector Machine, SVM）是一种二分类模型，其基本模型是定义在特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化。SVM 通过间隔最大化，可以使得模型对噪声更加鲁棒，从而提高模型的泛化能力。

和逻辑回归一样，支持向量机是一个二分类模型，且其也是个线性模型，即其分割超平面为 ${\mathbf{w}}^T\mathbf{x}+b=0$。我们可以将数据集分为两类，一类为正类，一类为负类。

在下面我们将首先讨论线性可分情况下的支持向量机。再介绍线性不可分的情况。

基础想法

我们考虑分类算法，我们只是关注是否所有的数据点被正确分类了，而并不在乎我们到底选择了哪一个（超）平面用于用于分隔数据点。但是支持向量机不仅仅关注分类是否正确，还关注分类的边界。我们希望分类的边界尽可能远离数据点，这样可以使得模型对噪声更加鲁棒，从而提高模型的泛化能力。

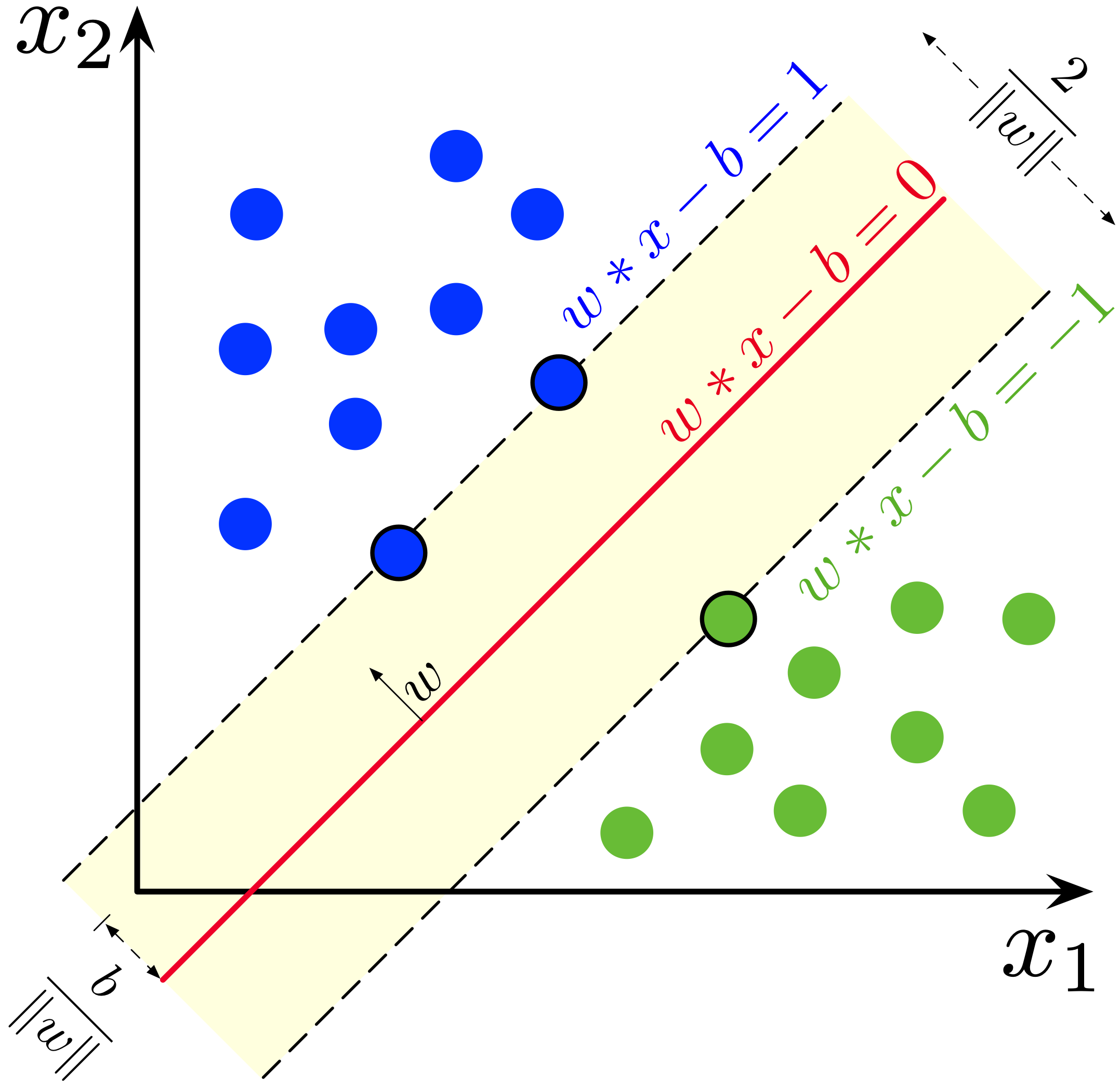
[https://en.m.wikipedia.org/wiki/File:SVM_margin.png]

上图是 SVM 的示例图。红色线是我们的假说。蓝色点为正类，绿色点为负类。黄色区域则是由离假说最近的正类和负类点组成的间隔（Margin）。间隔线（虚线）与假说平行，而在间隔线上的数据点，我们称其为支持向量（Support Vector）。我们希望寻找一个假说可以将两个类被正确分开，且能够使这个间隔最大化。

而因此，我们定义了新的假说：

$$\begin{array}{c}h(\mathbf{x})=\{\begin{array}{rl}+1& \text{ if }{\mathbf{w}}^T\mathbf{x}+b>0\\ -1& \text{ if }{\mathbf{w}}^T\mathbf{x}+b<0\end{array}\end{array}$$

即，如果这个点在超平面的上侧，我们将其分类为正类，否则分类为负类。

点到平面的距离

在一切开始前，我需要先介绍一下点到（超）平面（后简称平面）的距离。

我们定义平面 $H$ 为 ${\mathbf{w}}^T\mathbf{x}+b=0$。 并定义点 $Q$ $(q_1,q_2,q_3,...,q_N)$ 到平面 $H$ 的距禽为 $\text{dist}(Q,H)$。

我们想要知道怎么计算点 $Q$ 到平面 $H$ 的距离。

取平面任意一点 $P$ $(p_1,p_2,p_3,...,p_N)$，且因为平面上的点满足 ${\mathbf{w}}^T\mathbf{x}+b=0$，因此有 ${\mathbf{w}}^T\mathbf{p}+b=0$。

向量 $\overrightarrow{PQ}=\mathbf{q}-\mathbf{p}$，其相对于平面法向量的投影为 $|\overrightarrow{PQ}|\cos \theta$，其中 $\theta$ 为 $\overrightarrow{PQ}$ 和 $\mathbf{w}$ 的夹角。考虑其投影的几何性质，我们可以得到 $\text{dist}(Q,H)=|\overrightarrow{PQ}|\cos \theta$。

令法向量 $\mathbf{n}\perp H:(w_1,w_2,...,w_n)$，有

$$\begin{array}{rl}\overrightarrow{PQ}\cdot \mathbf{n}& =|\overrightarrow{PQ}||\mathbf{n}|\cos \theta \\ |\overrightarrow{PQ}|\cos \theta & =\frac{\mathbf{n}}{|\mathbf{n}|}\cdot \overrightarrow{PQ}\end{array}$$

因此则有：

$$\begin{array}{rl}\text{dist}(Q,H)& =\frac{\mathbf{n}}{|\mathbf{n}|}\cdot \overrightarrow{PQ}\\ & =\frac{\mathbf{w}}{||\mathbf{w}||}\cdot (\mathbf{q}-\mathbf{p})\\ & =\frac{1}{||\mathbf{w}||}\cdot ({\mathbf{w}}^T\mathbf{q}-{\mathbf{w}}^T\mathbf{p})\\ & =\frac{1}{||\mathbf{w}||}\cdot ({\mathbf{w}}^T\mathbf{q}+b-({\mathbf{w}}^T\mathbf{p}+b))\\ \because & {\mathbf{w}}^T\mathbf{p}+b=0\\ \therefore \text{dist}(Q,H)& =\frac{1}{||\mathbf{w}||}\cdot ({\mathbf{w}}^T\mathbf{q}+b)\\ & =\frac{{\mathbf{w}}^T\mathbf{q}+b}{||\mathbf{w}||}\end{array}$$

定义间隔（Margin）

根据上一节，我们可以定义距离公式：

$$\begin{array}{rl}& \text{dist}(h,{\mathbf{x}}_i)=\frac{\mid h({\mathbf{x}}_i)\mid }{||\mathbf{w}||}\end{array}$$

我们定义距离

$$\begin{array}{rl}{d}_i& =\text{dist}(h,{\mathbf{x}}_i)\\ & =\frac{\mid h({\mathbf{x}}_i)\mid }{||\mathbf{w}||}\end{array}$$

考虑 $y\in \{-1,+1\}$，因此由：

$$\begin{array}{c}{y}_i=\{\begin{array}{rl}+1& \text{ if }{\mathbf{w}}^T{\mathbf{x}}_i+b>0\text{分类正确}\\ -1& \text{ if }{\mathbf{w}}^T{\mathbf{x}}_i+b<0\text{分类正确}\\ +1& \text{ if }{\mathbf{w}}^T{\mathbf{x}}_i+b\le 0\text{分类错误}\\ -1& \text{ if }{\mathbf{w}}^T{\mathbf{x}}_i+b\ge 0\text{分类错误}\end{array}\end{array}$$

即如果分类正确，$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0$，如果分类错误，$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\le 0$。考虑 $y_i\in \{+1,-1\}$，即乘上它只会改变 ${\mathbf{w}}^T{\mathbf{x}}_i+b$ 的正负号而不会改变其绝对值，因此如果所有点都被正确分类，我们可以把边距改写为

$$\begin{array}{rl}{d}_i=\frac{\mid h({\mathbf{x}}_i)\mid }{||\mathbf{w}||}& =\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{||\mathbf{w}||}\\ & \Downarrow \\ d_i& =\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{||\mathbf{w}||}\\ s.t.\forall & ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

经过此变换，我们可以得到一个更加简洁的表达式：

$$\begin{array}{rl}& d_i=\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{||\mathbf{w}||}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

定义原问题 Prime Problem

我们的目标是最大化最小的间隔，即我们要先找到最小的间隔 ${\gamma }_n={\min }_n{d}_n$，然后寻找使其最大的参数 $\mathbf{w}$ 和 $b$。因此我们可以定义原问题为：

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\{\underset{n}{\min }{d}_n\}\\ \text{where}& d_n=\frac{y_n({\mathbf{w}}^T{\mathbf{x}}_n+b)}{||\mathbf{w}||}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

即

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\left\{\underset{n}{\min }\frac{y_n({\mathbf{w}}^T{\mathbf{x}}_n+b)}{||\mathbf{w}||}\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

由于在求最小点的时候，我们固定了 $\mathbf{w}$ ，因此我们可以把 $\mathbf{w}$ 提出来，即

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\left\{\frac{1}{||\mathbf{w}||}\underset{n}{\min }{y}_n({\mathbf{w}}^T{\mathbf{x}}_i+b)\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

考虑如果存在 $\mathbf{w}$ 和 $b$ 能满足超平面。则超平面可以被定义为

$$\begin{array}{r}{\mathbf{w}}^T\mathbf{x}+b=0\end{array}$$

如果我们对 $\mathbf{w}$ 和 $b$ 进行缩放，即 $\mathbf{w}\Rightarrow k\mathbf{w}$，$b\Rightarrow kb$，这样我们可以得到

$$\begin{array}{rl}(k\mathbf{w}{)}^T\mathbf{x}+kb& =0\\ k({\mathbf{w}}^T\mathbf{x}+b)& =0\end{array}$$

如果我们考虑最小边距的点，即 ${\min }_n{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)$，考虑总是存在常量 $k$ 使得${\min }_n{y}_n(k{\mathbf{w}}^T{\mathbf{x}}_n+kb)=1$，因此我们可以对平面进行乘 $k$变换，因此有 ${\min }_n{y}_n({\mathbf{w}}^T{\mathbf{x}}_n+b)=1$。而由于最小化的边距被定义为了 $1$，因此约束条件被改写为 $$\begin{array}{rl}s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)\ge 1\end{array}$$

因此我们可以改写原问题为

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\left\{\frac{1}{||\mathbf{w}||}\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)\ge 1\end{array}$$

边界 $\gamma$ 被定义为 $$\gamma =\frac{1}{||\mathbf{w}||}$$ 而最大化一个数的倒数等价于最小化这个数的倒数的倒数，即 $$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{||\mathbf{w}||\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)\ge 1\end{array}$$

考虑我们最小化一个绝对值，也就在最小化这个绝对值的平方，因此有：

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{||\mathbf{w}|{|}^2\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)\ge 1\end{array}$$

为了方便之后的求导，我们可以把最小化的平方乘上一个正系数 $\frac{1}{2}$，即：

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.y_{i}h({\mathbf{x}}_i)>0\end{array}$$

我们对 $\mathbf{x}$ 进行非线性变换，即 $\mathbf{x}\Rightarrow \varphi (\mathbf{x})$，这样我们可以得到

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.\\ & y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)\ge 1\end{array}$$

我们需要优化这个函数

改写为对偶问题 Dual Problem

考虑原问题

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2\right\}\\ s.t.& \forall ({\mathbf{x}}_i,y_i)\in \mathcal{D}.\\ & y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)\ge 1\end{array}$$

由于约束比较复杂，我们难以直接优化。因此我们需要改写原问题以方便优化。

我们可以定义一个惩罚函数 $g(\mathbf{w},b)$，当违反约束时，这个惩罚会很大，而当满足约束时，这个惩罚会很小。因此在优化这个整体问题时，我们也在优化惩罚函数，即尽可能符合约束。即我们可以定义把原问题重新写为：

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2+g(\mathbf{w},b)\right\}\end{array}$$ 如果我们能将约束转化为上述的 $g$ 函数，则我们就可以把原问题转化为一个无约束问题。因此我们需要构建惩罚函数 $g$。

惩罚函数

我们首先改写约束条件：

$$\begin{array}{rl}{y}_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)& \ge 1\\ & \Downarrow \\ y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)-1& \ge 0\\ & \Downarrow \\ 1-y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b)& \le 0\end{array}$$

我们可以定义惩罚函数为

$$\begin{array}{rl}& g(\mathbf{w},b)=\sum _{i=1}^N{\alpha }_i(1-y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b))\\ s.t.& {\alpha }_i\ge 0\end{array}$$

在这里，我们称 ${\alpha }_i$ 为拉格朗日乘子。（因为这个方法本质上被称为拉格朗日乘子法）且其：

1. 当 ${\mathbf{x}}_i$ 不是支持向量，即 ${\alpha }_i=0$，这个点对于最终的分类没有影响
2. 当 ${\mathbf{x}}_i$ 是支持向量，即 ${\alpha }_i>0$，这个点对于最终的分类有影响

当 ${\alpha }_i>0$ 时，我们称 ${\mathbf{x}}_i$ 为支持向量。需要注意的是尽管有可能 ${\mathbf{x}}_i$ 在边界上，但是其 ${\alpha }_i$ 仍然可能为 $0$。

我们希望使得所有违反约束的点的惩罚尽可能大，即我们希望最大化这些惩罚，因此我们可以改写惩罚函数为：

$$\begin{array}{rl}& g(\mathbf{w},b)=\max \sum _{i=1}^N{\alpha }_i(1-y_i({\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b))\\ s.t.& {\alpha }_i\ge 0\end{array}$$

我们将惩罚函数带入原问题，我们可以得到：

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2+\underset{\alpha }{\max }\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b))\right\}\\ s.t.& y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\ge 1\\ & {\alpha }_n\ge 0\end{array}$$

由于内侧优化 ${\max }_{\alpha }$ 并不会影响到 $\frac{1}{2}||\mathbf{w}|{|}^2$，因此可以提出来，即： $$\begin{array}{rl}& \underset{\mathbf{w},b}{\min }\underset{\alpha }{\max }\left\{\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b))\right\}\\ s.t.& y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\ge 1\\ & {\alpha }_n\ge 0\end{array}$$

根据一些数学推导，我们可以得到最终的优化问题为：

$$\begin{array}{rl}& \underset{\alpha }{\max }\underset{\mathbf{w},b}{\min }\left\{\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b))\right\}\\ s.t.& y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\ge 1\\ & {\alpha }_n\ge 0\end{array}$$

即： $$\begin{array}{rl}& \underset{\alpha }{\max }\underset{\mathbf{w},b}{\min }\mathcal{L}(\alpha ,\mathbf{w},b)=\left\{\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b))\right\}\\ s.t.& y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\ge 1\\ & {\alpha }_n\ge 0\end{array}$$

改写对偶问题

我们对其进行求导，即

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial \mathbf{w}}& =\mathbf{w}-\sum _{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)\\ \frac{\partial \mathcal{L}}{\partial b}& =-\sum _{n=1}^N{\alpha }_n{y}_n\end{array}$$

如果损失最小，我们可以得到：

$$\begin{array}{ccc}\frac{\partial \mathcal{L}}{\partial \mathbf{w}}=0& \Rightarrow & \mathbf{w}={\sum }_{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)\\ & & \\ \frac{\partial \mathcal{L}}{\partial b}=0& \Rightarrow & {\sum }_{n=1}^N{\alpha }_n{y}_n=0\end{array}$$

将 $\mathbf{w}$ 和 $b$ 代入 $\mathcal{L}$，我们可以把优化问题改写为

$$\begin{array}{rl}& \underset{\alpha }{\mathrm{argmax}}\mathcal{L}(\alpha )=\sum _{n=1}^N{\alpha }_n-\frac{1}{2}\sum _{n=1}^N\sum _{m=1}^N{\alpha }_n{\alpha }_m{y}_n{y}_m\varphi ({\mathbf{x}}_n{)}^T\varphi ({\mathbf{x}}_m)\\ s.t.& {\alpha }_n\ge 0\\ & \sum _{n=1}^N{a}_n{y}_n=0\end{array}$$

定义核函数 $\kappa ({\mathbf{x}}_n,{\mathbf{x}}_m)=\varphi ({\mathbf{x}}_n{)}^T\varphi ({\mathbf{x}}_m)$，可以把优化问题改写为

$$\begin{array}{rl}& \underset{\alpha }{\mathrm{argmax}}\mathcal{L}(\alpha )=\sum _{n=1}^N{\alpha }_n-\frac{1}{2}\sum _{n=1}^N\sum _{m=1}^N{\alpha }_n{\alpha }_m{y}_n{y}_m\kappa ({\mathbf{x}}_n,{\mathbf{x}}_m)\\ s.t.& {\alpha }_n\ge 0\\ & \sum _{n=1}^N{a}_n{y}_n=0\\ \text{where}& \kappa ({\mathbf{x}}_n,{\mathbf{x}}_m)=\varphi ({\mathbf{x}}_n{)}^T\varphi ({\mathbf{x}}_m)\end{array}$$

预测

原问题的预测是很直觉的，即：

$$\begin{array}{rl}{\text{predict}}_{prime}(\mathbf{x})& =\text{sign}(h(\mathbf{x}))\\ & =\text{sign}({\mathbf{w}}^T\varphi (\mathbf{x})+b)\\ & =\text{sign}\left(\sum _{n=1}^N{\alpha }_n{y}_n\kappa ({\mathbf{x}}_n,\mathbf{x})+b\right)\end{array}$$

其中 $\text{sign}$ 为符号函数，即如果输入为正数，则输出为 $+1$，否则输出为 $-1$。

而对偶问题的预测有所不同。由于我们有 $\mathbf{w}={\sum }_{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)$，我们将其带入 $h(\mathbf{x})$，我们可以得到：

$$\begin{array}{rl}h(\mathbf{x})& ={\mathbf{w}}^T\varphi (\mathbf{x})+b\\ & ={\left(\sum _{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)\right)}^T\varphi (\mathbf{x})+b\\ & =\sum _{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n{)}^T\varphi (\mathbf{x})+b\\ & =\sum _{n=1}^N{\alpha }_n{y}_n\kappa ({\mathbf{x}}_n,\mathbf{x})+b\end{array}$$

$$\begin{array}{rl}{\text{predict}}_{dual}(\mathbf{x})& =\text{sign}(h(\mathbf{x}))\\ & =\text{sign}\left(\sum _{n=1}^N{\alpha }_n{y}_n\kappa ({\mathbf{x}}_n,\mathbf{x})+b\right)\end{array}$$

软间隔 Soft Margin

但是如果遇到非线性可分情况，我们需要引入软间隔（Soft Margin）。我们可以引入一个松弛变量 ${\xi }_n$，其可以使得一些点可以在越过边界的情况下被正确分类。我们可以定义新的约束条件：

$$\begin{array}{rl}\forall & n\in \{1,2,...,N\}.\\ & y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\ge 1-{\xi }_n\\ & {\xi }_n\ge 0\end{array}$$

即

$$\begin{array}{rl}\forall & n\in [1,N].\\ & y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)+{\xi }_n\ge 1({\xi }_n\ge 0)\end{array}$$

而其实我们本质期望这个松弛变量 ${\xi }_n$ 越小越好，因此我们可以定义惩罚函数 $g_{\xi }$ 为：

$$\begin{array}{r}{g}_{\xi }=C\sum _{n=1}^N{\xi }_n\end{array}$$

其中 $C$ 为一个超参数（hyperparameter），其可以控制惩罚的大小。我们可以把原问题改写为：

$$\begin{array}{rl}& \underset{\mathbf{w},b,\xi }{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n\right\}\\ s.t.& \forall n\in [1,N].\\ & y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)+{\xi }_n\ge 1\\ & {\xi }_n\ge 0\end{array}$$

我们可以将问题逐步改写为对偶问题以方便求解：

$$\begin{array}{rl}& \underset{\mathbf{w},b,\xi }{\mathrm{argmin}}\left\{\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n\right\}\\ s.t.& \forall n\in [1,N].\\ & 1-{\xi }_n-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)\le 0\\ & -{\xi }_n\le 0\end{array}$$

改写为拉格朗日乘子法为：

$$\begin{array}{rl}\mathcal{L}& =\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n-\sum _{n=1}^N{\beta }_n{\xi }_n+\sum _{n=1}^N{\alpha }_n[1-{\xi }_n-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ \text{where}& {\alpha }_n\ge 0\\ & {\beta }_n\ge 0\end{array}$$ 和线性可分情况类似（即没有软间隔的情况，也被称为硬间隔），我们的优化问题因此被转化为： $$\begin{array}{rlrl}& \underset{\alpha }{\max }\underset{\mathbf{w},b}{\min }\mathcal{L}& & \underset{\mathbf{w},b}{\min }\underset{\alpha }{\max }\mathcal{L}\\ \text{where}& {\alpha }_n\ge 0& \text{where}& {\alpha }_n\ge 0\\ & {\beta }_n\ge 0& & {\beta }_n\ge 0\\ & y_n({\mathbf{w}}^T{\mathbf{x}}_n)\ge 1+{\xi }_n& & y_n({\mathbf{w}}^T{\mathbf{x}}_n)\ge 1+{\xi }_n\end{array}$$ 上述两个问题是等价的（Minimax Theorem）。

而如果我们对此拉格朗日乘子法取最低点，即为 $$\begin{array}{ccccc}\frac{\partial \mathcal{L}}{\partial \mathbf{w}}=0& \Rightarrow & \mathbf{w}-{\sum }_{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)=0& \Rightarrow & \mathbf{w}={\sum }_{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)\\ \frac{\partial \mathcal{L}}{\partial {\xi }_n}=0& \Rightarrow & C-{\beta }_n-{\alpha }_n=0& \Rightarrow & {\alpha }_n+{\beta }_n=C\\ \frac{\partial \mathcal{L}}{\partial b}=0& \Rightarrow & -{\sum }_{n=1}^N{\alpha }_n{y}_n=0& \Rightarrow & {\sum }_{n=1}^N{\alpha }_n{y}_n=0\end{array}$$

其中 ${\alpha }_n+{\beta }_n=C$ 可以改写为 ${\alpha }_n=C-{\beta }_n$，考虑 ${\beta }_n\ge 0$

因此则有 ${\alpha }_n\in [0,C]$。我们称这一条限制为 Box Constraint。

$$\begin{array}{rl}\mathcal{L}& =\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n-\sum _{n=1}^N{\beta }_n{\xi }_n+\sum _{n=1}^N{\alpha }_n[1-{\xi }_n-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n-\sum _{n=1}^N{\beta }_n{\xi }_n-\sum _{n=1}^N{\alpha }_n{\xi }_n+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n-\sum _{n=1}^N({\alpha }_n+{\beta }_n){\xi }_n+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ \because & {\alpha }_n+{\beta }_n=C\\ \therefore & =\frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{n=1}^N{\xi }_n-\sum _{n=1}^{N}C{\xi }_n+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n)+b)]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n))-y_{n}b]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n))]-\sum _{n=1}^N{\alpha }_n{y}_{n}b\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n))]-b\sum _{n=1}^N{\alpha }_n{y}_n\\ \because & \sum _{n=1}^N{\alpha }_n{y}_n=0\\ \therefore & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n[1-y_n({\mathbf{w}}^T\varphi ({\mathbf{x}}_n))]\\ & =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n-\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)\end{array}$$

因此这个公式可以被拆成三部分：

• $\frac{1}{2}||\mathbf{w}|{|}^2$​
• ${\sum }_{n=1}^N{\alpha }_n$
• $-{\sum }_{n=1}^N{\alpha }_n{y}_n{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)$​

我们对第一项进行修改 $$\begin{array}{rl}& \frac{1}{2}||\mathbf{w}|{|}^2=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\\ \because & \mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n\varphi ({\mathbf{x}}_n)\\ \therefore & \frac{1}{2}||\mathbf{w}|{|}^2=\frac{1}{2}{\left(\sum _{i=1}^N{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i)\right)}^T\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\mathbf{x}}_j)\right)\end{array}$$

$$\begin{array}{rl}\frac{1}{2}||\mathbf{w}|{|}^2& =\frac{1}{2}{\left(\sum _{i=1}^N{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i)\right)}^T\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\mathbf{x}}_j)\right)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)\end{array}$$

我们对第三项进行修改 $$\begin{array}{rl}-\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)& =-\sum _{n=1}^N{\alpha }_n{y}_n{\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\mathbf{x}}_j)\right)}^T\varphi ({\mathbf{x}}_n)\\ & =-\sum _{i=1}^N{\alpha }_i{y}_i{\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\mathbf{x}}_j)\right)}^T\varphi ({\mathbf{x}}_i)\\ & =-\sum _{i=1}^N{\alpha }_i{y}_i\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\mathbf{x}}_j{)}^T\varphi ({\mathbf{x}}_i)\right)\\ & =-\sum _{i=1}^N{\alpha }_i{y}_i\left(\sum _{j=1}^N{\alpha }_j{y}_j\kappa ({\mathbf{x}}_j,{\mathbf{x}}_i)\right)\\ & =-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{y}_i{\alpha }_j{y}_j\kappa ({\mathbf{x}}_j,{\mathbf{x}}_i)\\ & =-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)\end{array}$$ 将改写好的量带入： $$\begin{array}{rl}\mathcal{L}& =\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{n=1}^N{\alpha }_n-\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)+\sum _{n=1}^N{\alpha }_n-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)\\ & =\sum _{n=1}^N{\alpha }_n-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)\end{array}$$ 而我们的目标为最大化 $\mathcal{L}$，即 $$\begin{array}{rl}& \underset{\alpha }{\max }\mathcal{L}(\alpha )\\ s.t.& 0\le {\alpha }_i\le C\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$ 更完整地

$$\begin{array}{rl}& \underset{\alpha }{\max }\sum _{n=1}^N{\alpha }_n-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)\\ s.t.& {\alpha }_i\in [0,C]\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$

即我们可以定义优化问题为：

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)-\sum _{n=1}^N{\alpha }_n\\ s.t.& {\alpha }_i\in [0,C]\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$

而目标函数为：

$$J=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)-\sum _{n=1}^N{\alpha }_n$$

SMO 算法

通过上述过程，我们获得了我们需要优化的问题：

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)-\sum _{n=1}^N{\alpha }_n\\ s.t.& {\alpha }_i\in [0,C]\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$ 相比于传统的直接使用梯度下降，SVM使用一个名为 SMO 算法。上述问题我们定义其为二次编程（QP）问题。SMO 是一个启发式算法，其将这个问题分解成很多子 QP 问题再逐个解决分析。其性能比直接梯度下降好很多。

我们的目标是通过选择 $\alpha$ 从而使这个问题最优化。

这个算法的核心想法是每一步，从 $\alpha$ 中选择两个 ${\alpha }_i$、${\alpha }_j$ 并让其他 $\alpha$ 固定，然后调整这两个参数。通过反复循环这个操作，完成整体优化。

即：

初始化 $\alpha$ 循环： 选择一对${\alpha }_i$、${\alpha }_j$ 保持其他 $\alpha$固定，优化 ${\alpha }_i$ 和 ${\alpha }_j$

选择 $\alpha$ ：最简单的做法是选择 ${\alpha }_i,{\alpha }_j\ne 0$ ，我们将在后面讨论具体应该怎么做

优化 $\alpha$​ ：

由于我们固定了 ${\alpha }_i,{\alpha }_i$ 以外的所有参数，因此有

$$\begin{array}{rl}\sum _{n=1}^N{\alpha }_n{y}_n& =0\\ {\alpha }_i{y}_i+{\alpha }_j{y}_j+\sum _{n\in [1,N];n\ne i,j}{\alpha }_n{y}_n& =0\\ {\alpha }_i{y}_i+{\alpha }_j{y}_j& =-\sum _{n\in [1,N];n\ne i,j}{\alpha }_n{y}_n\end{array}$$ 如果令 $\zeta =-{\sum }_{n\in [1,N];n\ne i,j}{\alpha }_n{y}_n$，则有： $${\alpha }_i{y}_i+{\alpha }_j{y}_j=\zeta$$

需要注意 $\zeta$ （zeta）和 $\xi$ （xi）并不是一个字母。  
$\xi$ 表示松弛变量  
$\zeta$ 表示一个常量

我们如果在更新 ${\alpha }_j$ ，我们可以计算其下界 $L$:

这里我们将拆分两种情况：$y_i=y_j$ 和 $y_i\ne y_j$

情况 $y_i=y_j$，我们有 ${\alpha }_i+{\alpha }_j=\zeta$ 或者 $-{\alpha }_i-{\alpha }_j=\zeta$ $$\begin{gathered} {\alpha }_i+{\alpha }_j=\zeta \Rightarrow {\alpha }_j=\zeta -{\alpha }_i \\ \begin{array}{rl}\because & {\alpha }_i\in [0,C]\\ & {\alpha }_j=\zeta -{\alpha }_i\\ & C\ge 0\\ \therefore & {\alpha }_j\in [\zeta -C,\zeta ]\\ \therefore & {\alpha }_j\in [{\alpha }_i+{\alpha }_j-C,{\alpha }_i+{\alpha }_j]\end{array} \end{gathered}$$

$$\begin{gathered} {\alpha }_i+{\alpha }_j=-\zeta \Rightarrow {\alpha }_j=-\zeta -{\alpha }_i \\ \begin{array}{rl}\because & {\alpha }_i\in [0,C]\\ & {\alpha }_j=-\zeta -{\alpha }_i\\ & C\ge 0\\ \therefore & {\alpha }_j\in [-\zeta -C,-\zeta ]\\ \therefore & {\alpha }_j\in [{\alpha }_i+{\alpha }_j-C,{\alpha }_i+{\alpha }_j]\end{array} \end{gathered}$$