凸函数(Convex)
定义
[https://en.wikipedia.org/wiki/Convex_function#/media/File:ConvexFunction.svg]
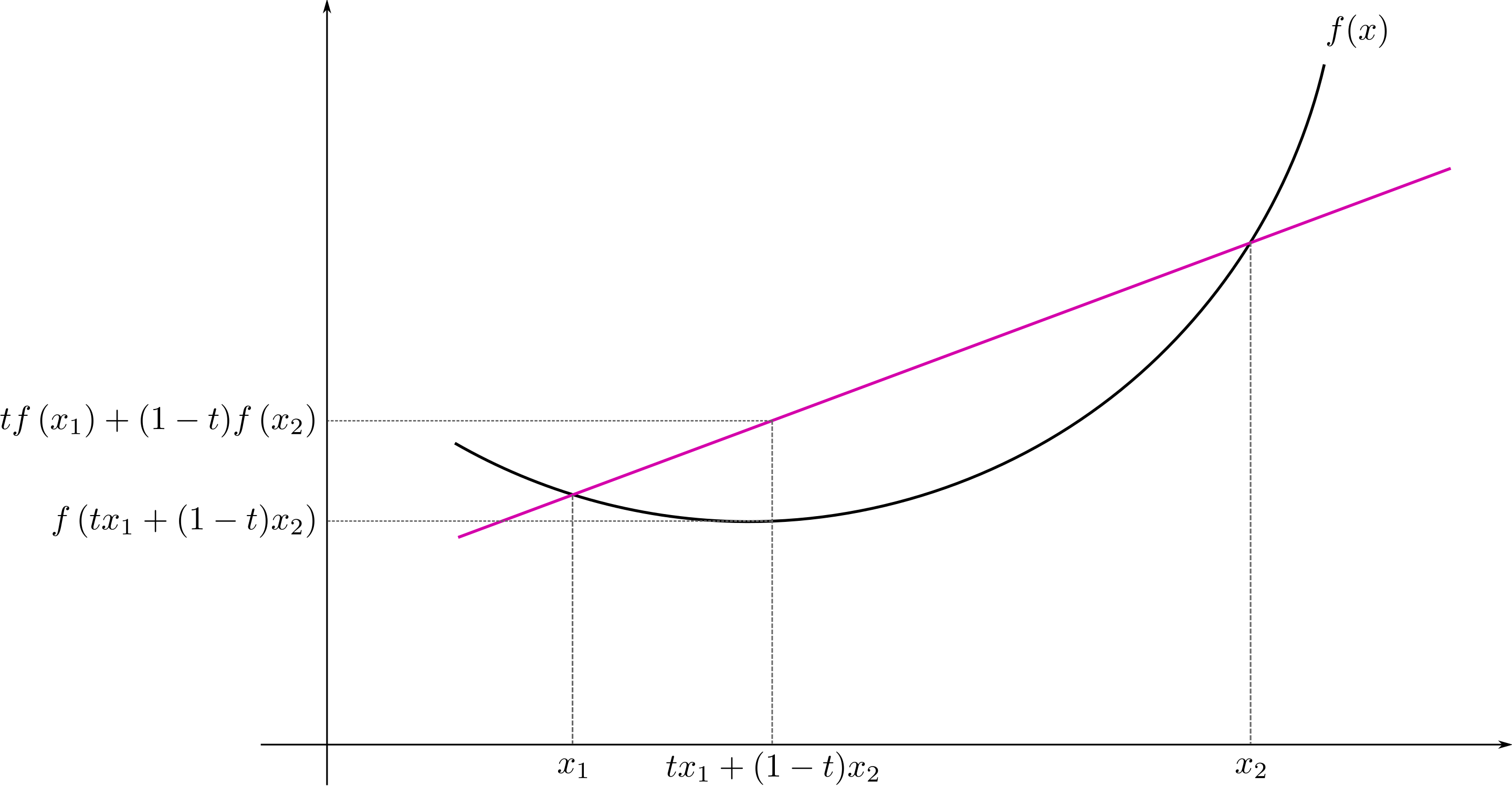
对于所有在 定义域内的 且 ,有:
则函数 是凸函数。
而如果在此基础上,当 时,有: 则函数 是严格的凸(strictly convex)函数。
其很好理解,左侧表示函数(图中黑线)在 区域的值,右侧表示线段的线性插值(图中玫红色值)。凸函数的定义即为:在 区域,函数上的值不会超过线性插值。
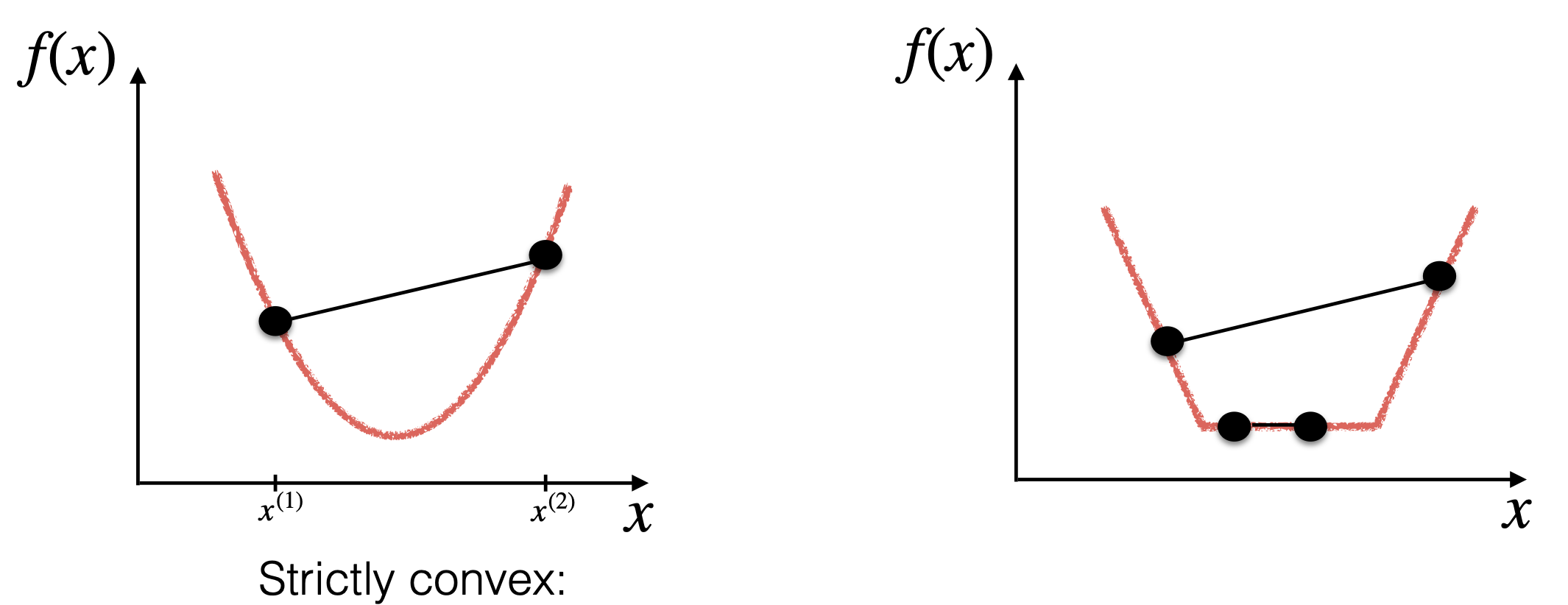 [Prof. Leandro L. Minku's slides]
[Prof. Leandro L. Minku's slides]
凸函数有一个很有用的性质:凸函数的局部最小值也是全局最小值。
并且如果函数是严格凸的,那么局部最小值是唯一的。
而对于凹函数,只需要将不等号反过来即可。即:
1 阶导
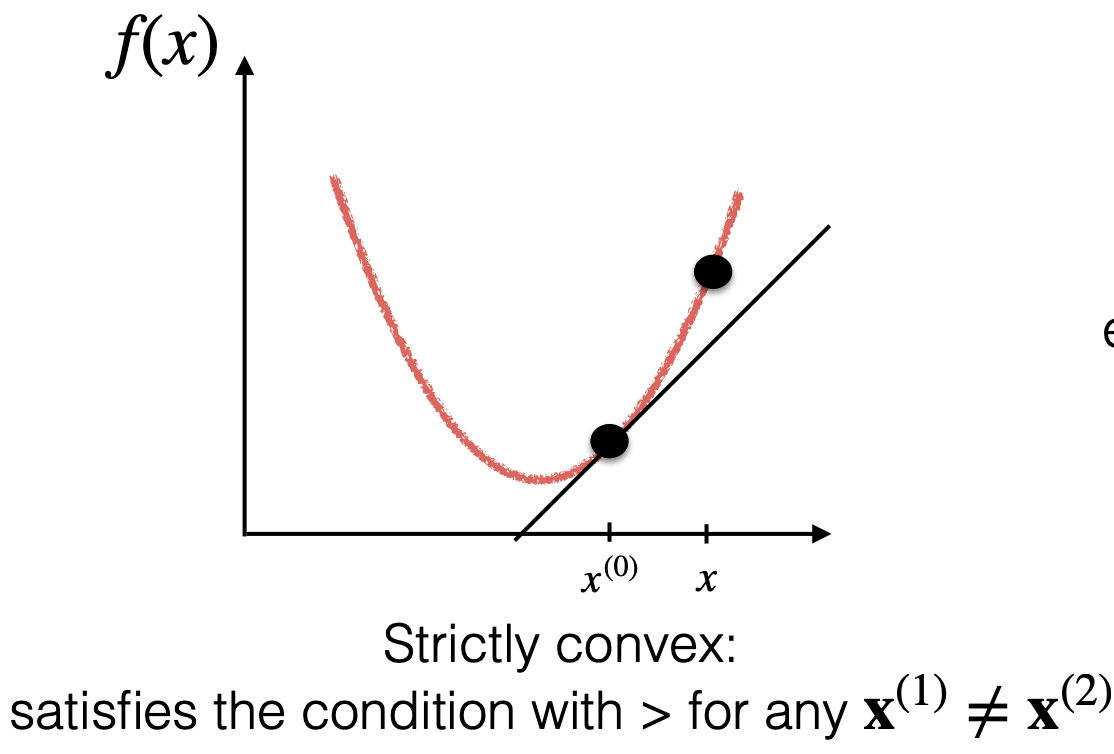
函数 是凸函数,当且仅当对于其定义域 为凸集且所有 满足:
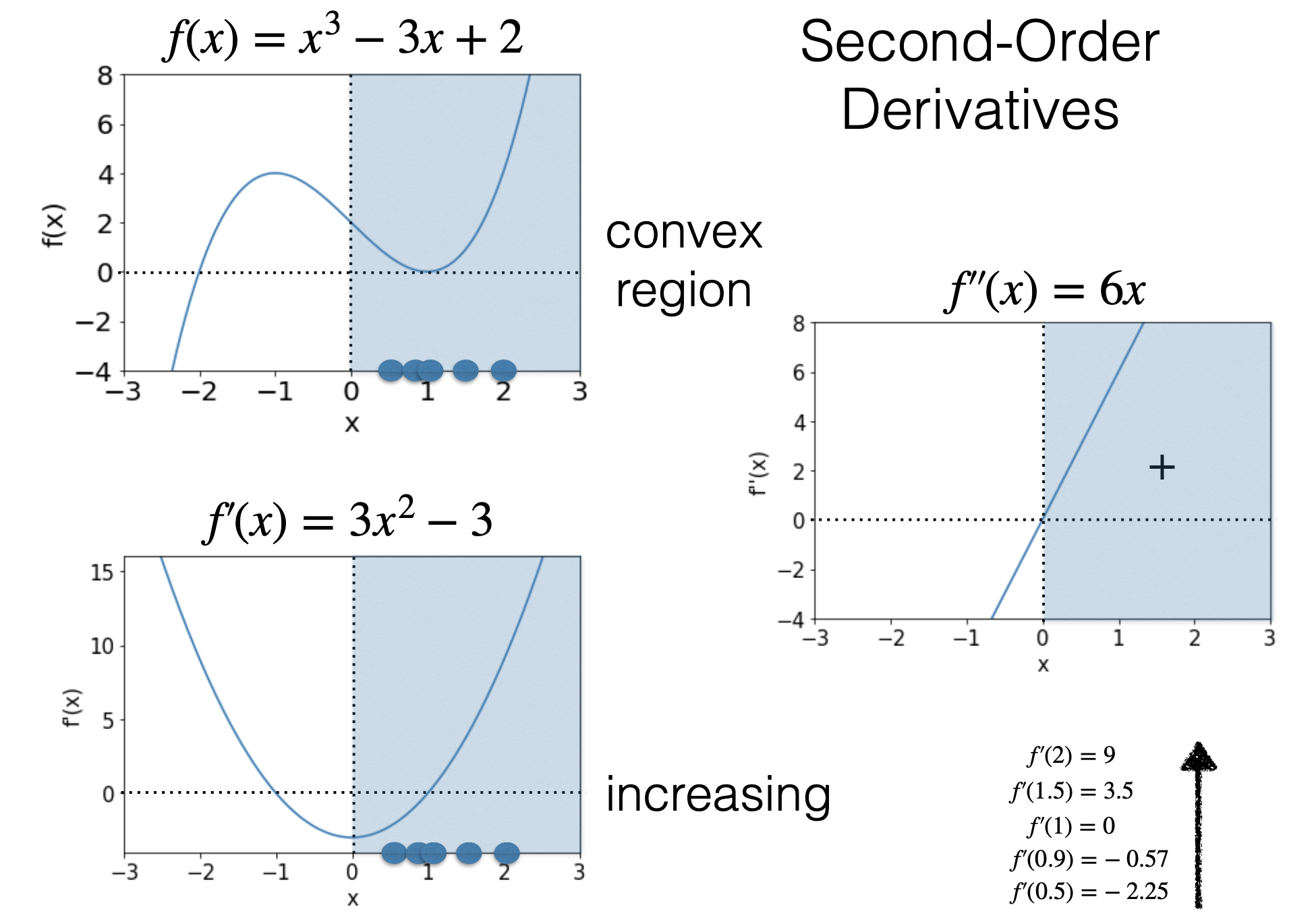
2 阶导
函数 是凸函数,当且仅当 是凸集并且其 (海森矩阵)对于任何 是半正定的(Positive Semidefinite, PSD)
如果(不是iff) 是凸集并且其 对于任何 是正定(Positive Definite, PD)的,则 为严格凸函数。
单变量场景
| 凸函数 | 凹函数 |
|---|---|
| 函数是凸的 | 函数是凹的 |
| 是凸的 是凹的 | 是凹的 是凸的 |
| 是严格凸的 | 是严格凹的 |
| 的局部最小值 | 是 的局部最大值 |
多变量场景
函数是凸的 iff 不再适用。
函数是凸的 iff (半正定,PSD)
半正定被定义为:
对称(symmetric)方阵( ) 是半正定的,当且仅当:
需要注意的是,如果一个 全为正数,也可能不是PSD。存在负数也不代表不能为 PSD。
