线性回归

什么是线性回归

线性回归（Linear Regression）是一个机器学习模型用于完成回归任务。为解释线性回归，我们将其分为两个部分：线性和回归。

[https://simple.wikipedia.org/wiki/Linear_regression#/media/File:Linear_regression.svg]

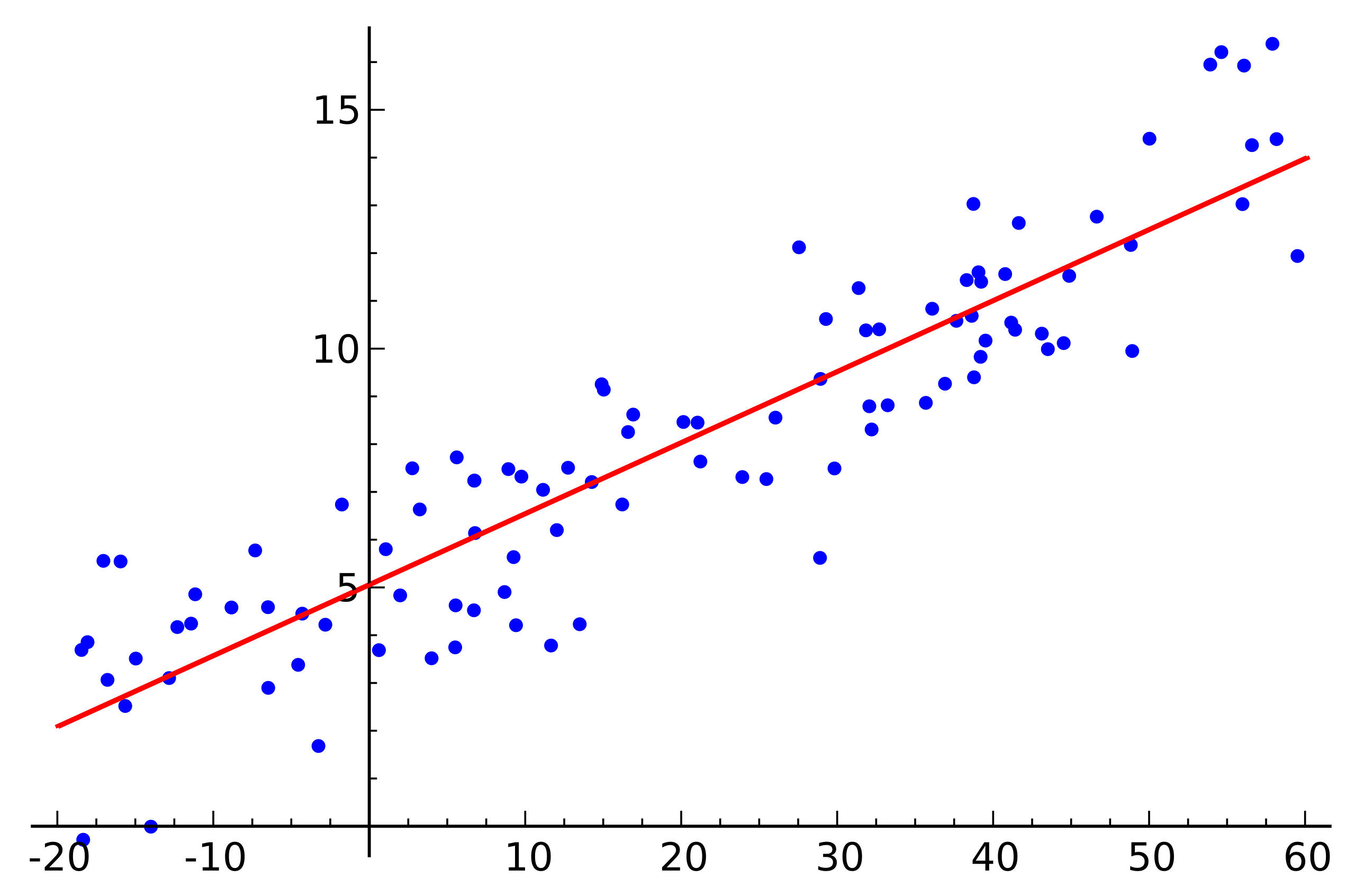
上图是线性回归的一个演示图。我们可以看到有很多点，和一根线。这根线就是我们的线性回归模型。我们称之为其是我们的假说。而这些点就是我们的数据集。我们的目标是找到一根线，使得这根线可以最好的拟合这些点（或者说，更好地服从数据点的趋势）。而用线去拟合这些点，我们就称之为回归。

而线性（Linear）则是指这个模型是一个线性函数（Linear function），其可以被定义为：

$$\begin{array}{rl}f(\mathbf{x})& =w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d+b\\ & =\left[\begin{array}{c}{w}_1,w_2,\dots ,w_d\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_d\end{array}\right]+b\\ & ={\mathbf{w}}^T\mathbf{x}+b\end{array}$$

用一维的例子解释，我们可以简易的认为对于输入的每一个特征 $x_i$，我们都会有一个权重 $w_i$，而我们的线性函数就是将所有的特征乘上对应的权重后相加，再加上一个偏置 $b$。而这个线性函数就是我们的线性回归模型。

即考虑一维线性函数 $y=kx+b$，我们可以将其改写为 $y=w_{1}x+b$，其中 $w_1=k$，$b$ 是偏置。而对于多维的情况，我们可以将其改写为 $y=w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d+b$。

如果我们假设 $x_0=1$，并令 $w_0=b$ 则我们可以认为

$$\begin{array}{rl}f(\mathbf{x})& =1\times b+w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d\\ & =b{x}_0+w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d\\ & =w_0{x}_0+w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d\\ & ={\mathbf{w}}^T\mathbf{x}\end{array}$$

其中 $\mathbf{w}$ 是一个 $d$ 维的向量，$\mathbf{x}$ 是一个 $d$ 维的向量，$w_i$ 是 $\mathbf{w}$ 的第 $i$ 个元素，$x_i$ 是 $\mathbf{x}$ 的第 $i$ 个元素。而 $f(\mathbf{x})$ 是我们的线性函数，其可以将输入 $\mathbf{x}$ 映射到一个标量值。

更严格的定义

向量我们可以认为一个有 $d$ 个数字的数组，而标量则是一个单独的数字。

我们需要从数据集尝试寻找参数使线性函数能够最好的拟合。我们可以定义数据集为：

$$\mathcal{D}=\{({\mathbf{x}}_1,y_1),\dots ,({\mathbf{x}}_N,y_N)\}$$

即数据集是由 $n$ 个数据点组成，每个数据点包含一个输入 ${\mathbf{x}}_i$ 和一个输出 $y_i$。而我们的目标是找到一个权重 $\mathbf{w}$，使得我们的线性函数 $f$ 能够最好的拟合数据集 $\mathcal{D}$。

用数学语言来描述，我们假设输入数据是一个 $d$ 维向量 $\mathbf{x}$，而输出数据是一个标量 $y$。我们可以定义输入空间 $\mathcal{X}$ 为一个 $d$ 维的实数空间，而输出空间 $\mathcal{Y}$ 为一个实数空间。即：

$$\begin{gathered} \mathcal{X}:{\mathbb{R}}^d\mathbf{x}\in {\mathbb{R}}^d \\ \mathcal{Y}:\mathbb{R}y\in \mathbb{R} \end{gathered}$$

而我们的线性函数 $f$ 可以被定义为是从输入空间 $\mathcal{X}$ 到输出空间 $\mathcal{Y}$ 的一个映射，即： $$f(\mathbf{x}):\mathcal{X}\in {\mathbb{R}}^d\to \mathcal{Y}\in \mathbb{R}$$

成本函数

那我们应该如何去寻找到最终最佳的$\mathbf{w}$呢？我们需要定义一个函数，叫损失函数。其用于衡量我们的预测值 $\hat{y}$ 与真实值 $y$ 之间的差距。如果我们能通过某些手段最小化这个损失函数，我们也就相当于让模型可以学习到最佳的$\mathbf{w}$。这个过程就是我们所说的训练过程。

而线性回归模型的损失应该怎么定义呢？相信聪明的朋友已经知道了！我们可以通过计算预测值与真实值之间的差距来定义损失函数。我们可以考虑 $y_i$ 与模型预测的 ${\hat{y}}_i$ 的距离，即 $\text{dist}(y,\hat{y})$。

如果我们的模型预测的值与真实值之间的距离越小，那么我们的模型就越好。因此我们可以定义距离函数为这两个点的几何距离，即欧式距离：

$$\begin{array}{rl}\text{dist}(y,\hat{y})& =|y-\hat{y}|\\ & =\sqrt{(y-\hat{y}{)}^2}\end{array}$$

其中我们将其转化为平方的形式，是因为平方相比于绝对值更容易求导，而且在求导的时候也不会受到绝对值的影响。

而上述式在最后进行平方根运算，而我们在求导的时候会遇到开方的问题，这会使得我们的求导变得复杂。因此我们可以将其转化为平方的形式，是因为平方相比于开方更容易求导，而且在求导的时候也不会受到开方的影响。而其与几何距离函数有着相同的单调性，这也意味着我们可以通过最小化平方距离 $dis{t}^{\prime }$ 来最小化几何距离。

因此我们可以定义距离函数为：

$${\text{dist}}^{\prime }(y,\hat{y})=(y-\hat{y}{)}^2$$

而考虑上式只考虑了一个样本，而我们的数据集中有多个样本，因此我们需要对所有的样本求平均值以得到平均损失。因此我们可以定义损失函数 $L$ 为：

$$\begin{array}{rl}L(y,\hat{y})& =\frac{1}{N}\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2\\ & =\frac{1}{n}\sum _{i=1}^n(y_i-{\mathbf{w}}^T{\mathbf{x}}_i{)}^2\end{array}$$

因此目前我们尝试寻找一个权重 $\mathbf{w}$ ，使其最小化成本函数 $$\underset{\mathbf{w}}{\min }\frac{1}{N}\sum _{i=1}^N(y_i-{\mathbf{w}}^T{\mathbf{x}}_i{)}^2$$ 为了方便后面的数学操作，我们可以将整个函数除以2，这样在后续求导的时候可以消去2，方便计算。而考虑乘上是一个正的常数，不会影响其的单调性与求导，也不会影响最小化这个式子的权重，因此我们可以将目标函数改写为 $$\begin{gathered} \underset{\mathbf{w}}{\min }\frac{1}{N}\sum _{i=1}^N(y_i-{\mathbf{w}}^T{\mathbf{x}}_i{)}^2 \\ \downarrow \\ \underset{\mathbf{w}}{\min }\frac{1}{2N}\sum _{i=1}^N(y_i-{\mathbf{w}}^T{\mathbf{x}}_i{)}^2 \\ J=\frac{1}{2N}\sum _{i=1}^N(y_i-{\mathbf{w}}^T{\mathbf{x}}_i{)}^2 \end{gathered}$$

优化目标函数

在完成问题的定义后，我们的目标转化成了最小化成本函数。在高中数学中，我们可以知道：一个函数的极值点只存在于导数为 0 的点。因此如果我们想获得一个参数使损失函数最小化，我们可以对成本函数求其求导数（更严谨来说，是对于成本函数的参数$\mathbf{w}$求偏导）。

易知该损失函数的极值点是全局最低点，故严格证明暂时略去。

简单来说，对于一个凸函数（convex function），其的全局最小值会出现在其导数为 0 的情况（需要注意的是，凸函数可能会有多个点使其导数为 0，且这些点的函数值均为全局最小值）。而我们的成本函数可以被证明为凸函数，因此我们可以通过对其求导数来获得全局最小值。我们会在后续章节讨论凸函数的性质。

$$\begin{array}{rl}\frac{\partial J}{\partial \mathbf{w}}& =\frac{\partial }{\partial \mathbf{w}}\frac{1}{2N}\sum _{i=1}^N({\mathbf{w}}^T{\mathbf{x}}_i-y_i{)}^2\\ & =\frac{\partial }{\partial \mathbf{w}}\frac{1}{2N}\sum _{i=1}^N({\mathbf{w}}^T{\mathbf{x}}_i{\mathbf{w}}^T{\mathbf{x}}_i+y_i^2-2{\mathbf{w}}^T{\mathbf{x}}_i{y}_i)\\ & =\frac{1}{2N}\sum _{i=1}^N(2{\mathbf{x}}_i^2\mathbf{w}-2{\mathbf{x}}_i{y}_i)\\ & =\frac{1}{N}\sum _{i=1}^N({\mathbf{x}}_i^2\mathbf{w}-{\mathbf{x}}_i{y}_i)\end{array}$$

求其极值点。令其偏导值为 0:

$$\begin{array}{rl}\frac{\partial J}{\partial \mathbf{w}}& =0\\ \frac{1}{N}\sum _{i=1}^N({\mathbf{x}}_i^2\mathbf{w}-{\mathbf{x}}_i{y}_i)& =0\\ \sum _{i=1}^N({\mathbf{x}}_i^2\mathbf{w}-{\mathbf{x}}_i{y}_i)& =0\\ \sum _{i=1}^N({\mathbf{x}}_i^2\mathbf{w})-\sum _{i=1}^N({\mathbf{x}}_i{y}_i)& =0\\ \mathbf{w}\sum _{i=1}^N({\mathbf{x}}_i^2)-\sum _{i=1}^N({\mathbf{x}}_i{y}_i)& =0\\ {\mathbf{w}}^{\ast }& =\frac{{\sum }_{i=1}^N{\mathbf{x}}_i{y}_i}{{\sum }_{i=1}^N{\mathbf{x}}_i^2}\end{array}$$

通过上述操作，我们可以获得最佳的${\mathbf{w}}^{\ast }$（星号 ${}^{\ast }$ 表示最佳），这个过程就是我们所说的训练过程。我们可以通过这个过程来训练我们的模型，使得模型可以学习到最佳的$\mathbf{w}$，从而可以对未知的数据进行预测。

由于我们可以通过代数直接获得函数的解析解，我们也称其为封闭解（Closed-form solution）。

需要注意的是并不是所有的问题都拥有封闭解，有些问题可能会有多个解，有些问题可能会有无穷个解，有些问题可能会没有解。而应对这种情况，我们会选择使用迭代的方法来求解（我们又称其为优化（Optimisation））。在后续的章节中，我们会介绍如何使用迭代的方法来求解线性回归问题。

矩阵形式

当然，为了方便实际运用，我们可以将整个过程用矩阵形式表达。

我们定义：

$$\begin{gathered} X=\left[\begin{array}{c}-{\mathbf{x}}_1^T-\\ -{\mathbf{x}}_2^T-\\ ⋮\\ -{\mathbf{x}}_N^T-\end{array}\right]\mathbf{y}=\left[\begin{array}{c}{y}_{(1)}\\ y_{(2)}\\ ⋮\\ y_{(N)}\end{array}\right]\mathbf{w}=\left[\begin{array}{c}b\\ w_{(1)}\\ w_{(2)}\\ ⋮\\ w_{(d)}\end{array}\right] \\ X\mathbf{w}=\left[\begin{array}{c}{\mathbf{x}}_1^T\mathbf{w}+b\\ {\mathbf{x}}_2^T\mathbf{w}+b\\ ⋮\\ {\mathbf{x}}_N^T\mathbf{w}+b\end{array}\right]X\mathbf{w}-\mathbf{y}=\left[\begin{array}{c}{\mathbf{x}}_1^T\mathbf{w}+b-y_{(1)}\\ {\mathbf{x}}_2^T\mathbf{w}+b-y_{(2)}\\ ⋮\\ {\mathbf{x}}_N^T\mathbf{w}+b-y_{(n)}\end{array}\right] \end{gathered}$$

因此有： $$\begin{array}{rl}(X\mathbf{w}-\mathbf{y}{)}^T(X\mathbf{w}-\mathbf{y})& ={\left[\begin{array}{c}{\mathbf{x}}_1^T\mathbf{w}+b-y_{(1)}\\ {\mathbf{x}}_2^T\mathbf{w}+b-y_{(2)}\\ ⋮\\ {\mathbf{x}}_N^T\mathbf{w}+b-y_{(n)}\end{array}\right]}^T\left[\begin{array}{c}{\mathbf{x}}_1^T\mathbf{w}+b-y_{(1)}\\ {\mathbf{x}}_2^T\mathbf{w}+b-y_{(2)}\\ ⋮\\ {\mathbf{x}}_N^T\mathbf{w}+b-y_{(n)}\end{array}\right]\\ & =\sum _{i=1}^N({\mathbf{x}}_i^T\mathbf{w}+b-y_{(i)}{)}^2\\ & =\sum _{i=1}^N({\mathbf{w}}^T{\mathbf{x}}_i-y_{(i)}{)}^2\\ & =2NJ\end{array}$$

其中 $J$ 是原来的损失函数。

因此有：

$$\begin{array}{rl}J& =\frac{1}{2N}(X\mathbf{w}-\mathbf{y}{)}^T(X\mathbf{w}-\mathbf{y})\\ & =\frac{1}{2N}({\mathbf{w}}^T{X}^{T}X\mathbf{w}-2{\mathbf{w}}^T{X}^T\mathbf{y}+{\mathbf{y}}^T\mathbf{y})\end{array}$$

对其求导：

$$\begin{array}{rl}\frac{\partial J}{\partial \mathbf{w}}& =\frac{\partial }{\partial \mathbf{w}}\left(\frac{1}{2N}({\mathbf{w}}^T{X}^{T}X\mathbf{w}-2{\mathbf{w}}^T{X}^T\mathbf{y}+{\mathbf{y}}^T\mathbf{y})\right)\\ & =\frac{1}{2N}\frac{\partial }{\partial \mathbf{w}}({\mathbf{w}}^T{X}^{T}X\mathbf{w}-2{\mathbf{w}}^T{X}^T\mathbf{y}+{\mathbf{y}}^T\mathbf{y})\\ & =\frac{1}{2N}(2X^{T}X\mathbf{w}-2X^T\mathbf{y})\end{array}$$

令导数为 0，我们可以得到：

$$\begin{array}{rl}{X}^{T}X\mathbf{w}-X^T\mathbf{y}& =0\\ X^{T}X\mathbf{w}& =X^T\mathbf{y}\\ \mathbf{w}& =\frac{X\mathbf{y}}{X^{T}X}\\ \mathbf{w}& =(X^{T}X{)}^{-1}{X}^T\mathbf{y}\end{array}$$

即：

$${\mathbf{w}}^{\ast }=(X^{T}X{)}^{-1}{X}^T\mathbf{y}$$

这就是我们的线性回归矩阵形式的解析解。