梯度下降 Gradient Descent

在上一节，我们通过线性回归了解了基础的监督学习的模型。我们定义了模型，成本函数，并尝试优化成本函数。优化成本函数使得我们的模型能够更好地完成任务（拟合数据）。在这一节，我们将介绍一个常用的优化算法：梯度下降（Gradient Descent）。其是一种更通用的方法用于最小化函数。

1. 梯度下降

初中和高中数学告诉我们，一个函数的斜率（即一阶导数）表示了函数的变化率。如果一个函数的斜率为正，那么函数在这一点上是递增的；如果一个函数的斜率为负，那么函数在这一点上是递减的。

对于函数 $f(x)$，如果我们在 $x=M$ 处有 $f^{\prime }(x)=0$，则其可能为极值。

若其是极大值，则我们可以得到：

而如果是极小值，则有：

梯度下降算法正是利用了这一点，通过不断地迭代，使得成本函数的值不断地减小。

我们假设我们需要寻找函数 $L(w)$ 的最小值，并且其的最小值与其的极小值重合。我们对其位于 $w_M$ 进行求导。因此我们可以得到三种情况：$L^{\prime }<0$，$L^{\prime }=0$，$L^{\prime }>0$。

我们使用图像来表示这三种情况。其中红线表示函数 $L(w)$，蓝线表示导数 $L^{\prime }(w)$。

情况 $L^{\prime }>0$：

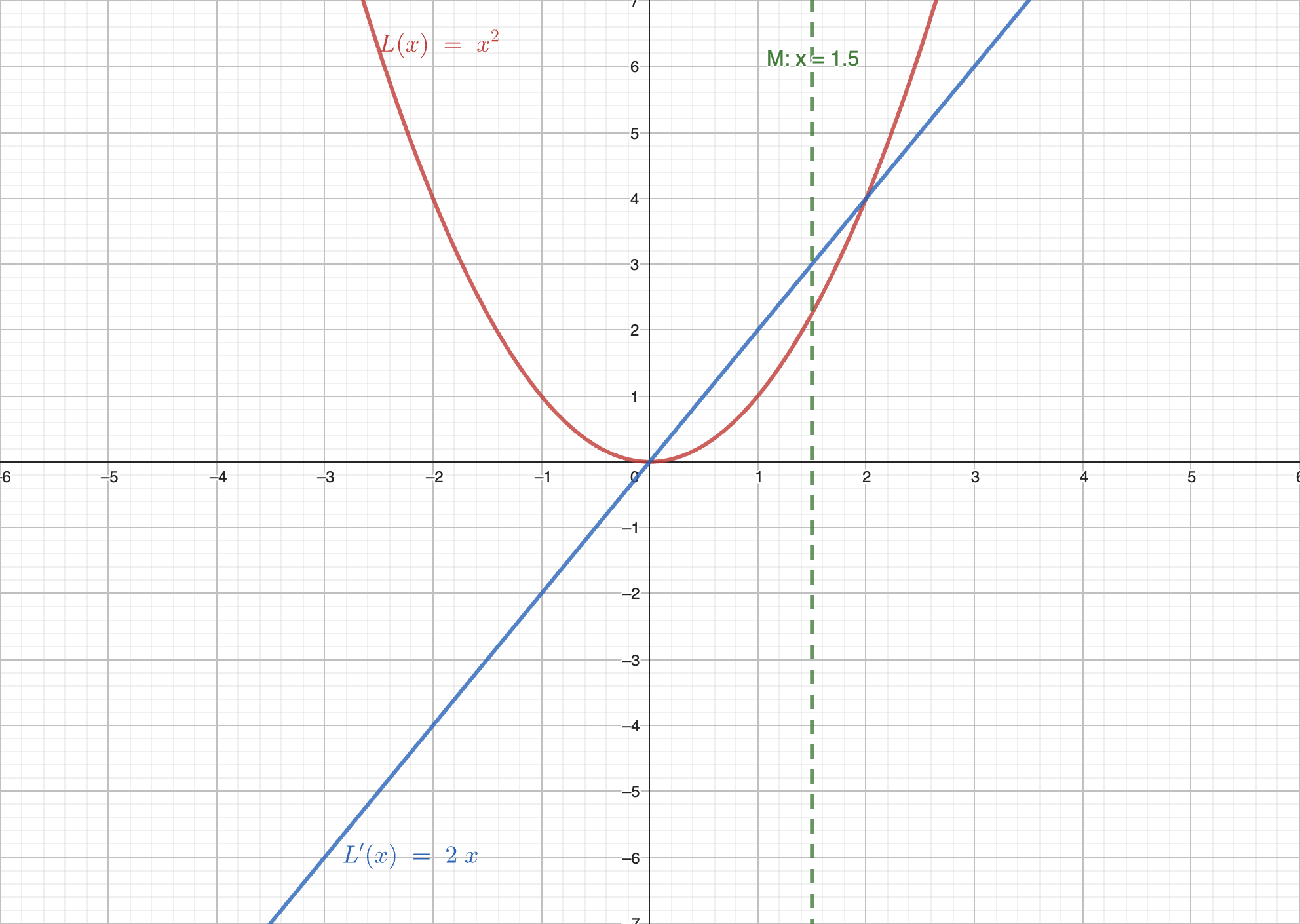
在这种情况下，导数大于 0。如果向右走，则函数的值增大，因此我们需要向左走。

情况 $L^{\prime }<0$：

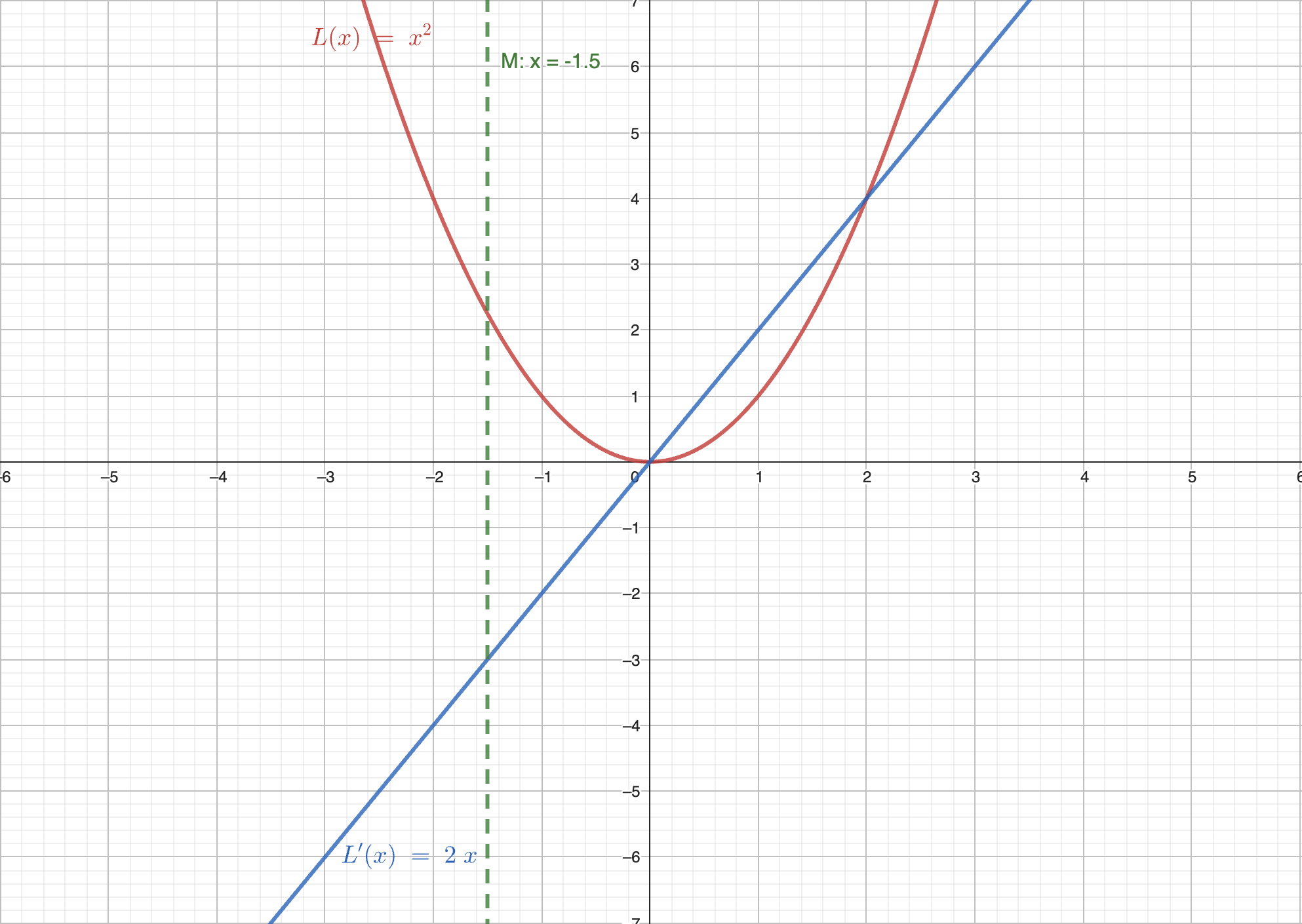
在这种情况下，导数小于 0。如果向左走，则函数的值增大，因此我们需要向右走。

情况 $L^{\prime }=0$：

在这种情况，我们已经到达了极值点。

经过上述实验，我们会发现函数极小值方向总是相对于当前位置的导数相反。即如果导数为正，我们需要向左走；如果导数为负，我们需要向右走。因此我们得到了梯度下降的更新公式：

$$\begin{array}{rl}w& =w-\eta L^{\prime }(w)\\ & =w-\eta \frac{dL}{dw}\end{array}$$

其中 $\eta$ 为学习率，其控制了我们每次更新的步长。越大的学习率，我们的步长越大，但是可能会导致我们错过最小值；越小的学习率，我们的步长越小，但是可能会导致我们收敛速度过慢。

如果考虑函数 $L$ 为多变量函数，我们则需要使用偏导替换导数。因此我们可以得到：

$$\begin{array}{rl}w& =w-\eta \frac{\partial L}{\partial w}\end{array}$$

但是考虑我们的参数 $\mathbf{w}$ 可能是一个向量，我们需要对每一个维度进行更新。因此我们可以得到：

$$\begin{array}{rl}{\mathbf{w}}_{(i)}& ={\mathbf{w}}_{(i)}-\eta \frac{\partial L}{\partial {\mathbf{w}}_{{}_{(i)}}}\end{array}$$

我们定义梯度 $\nabla L(\mathbf{w})$ 为：

$$\nabla L(\mathbf{w})=\begin{array}{c}\left[\begin{array}{c}\frac{\partial L}{\partial {\mathbf{w}}_{(1)}}\\ \frac{\partial L}{\partial {\mathbf{w}}_{(2)}}\\ ⋮\\ \frac{\partial L}{\partial {\mathbf{w}}_{(n)}}\end{array}\right]\end{array}$$

则我们可以得到最终的更新公式：

$$\begin{array}{rl}\mathbf{w}& =\mathbf{w}-\eta \nabla L(\mathbf{w})\end{array}$$

疑问

相信看到这的时，你一定有很多困惑。我将先解释几个最常见的问题。

Q: 如果我的函数极值点不是唯一的，梯度下降会怎么样？

梯度下降会收敛到一个局部最小值（即极值点）。这是因为梯度下降是一种贪心算法，其只会考虑当前的梯度，而不会考虑全局的梯度。

而解决的方法通常是一个叫“多次启动”的东西。其的做法是随机初始化参数，然后运行梯度下降。重复这个过程多次，然后选择最小的那个值。

Q: 如果我学到了极大值咋整？

在上述我们还有一种可能就是直接学习学到了 $\nabla L=0$ 且这个点是 $L$ 的极大值。这种情况通常建议去买个彩票（x）。使用多次启动可以解决这个问题。

Q：什么情况下梯度下降会失效？

梯度下降的一个前提是函数是可微的。如果函数不可微，梯度下降会失效。另外，如果函数的梯度变化很大，梯度下降也会失效。这种情况下，我们可以使用其他的优化算法，例如 IRLS。

Q：什么情况下梯度下降一定会收敛到最小值？

如果函数是凸函数，梯度下降一定会收敛到最小值。这是因为凸函数的局部最小值就是全局最小值。

（这个答案对欧皇无效）

原理：梯度下降为什么总是能走向最深的点

梯度下降的本质推导来源于泰勒展开。泰勒展开是一个非常重要的数学工具，它可以将一个函数在某一点附近用一个多项式来近似表示。泰勒展开的公式如下：

$$\begin{array}{rl}f(x)& =\sum _{n=0}^{\infty }\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n\\ & =f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n\end{array}$$

其将函数在 $x_0$ 处使用多阶导数展开，展开的多项式的次数为 $n$。换句话说如果我们一级展开，我们则需要使用 0 阶导数（函数值）和一阶导数（斜率）；如果我们二级展开，我们则需要使用 0 阶导数 $f^{(0)}(x)=f(x)$（函数值）、一阶导数 $f^{(1)}(x)=f^{\prime }(x)$（斜率）和二阶导数 $f^{(2)}(x)=f^{\prime \prime }(x)$（曲率，或者说，导数的导数）以此类推。

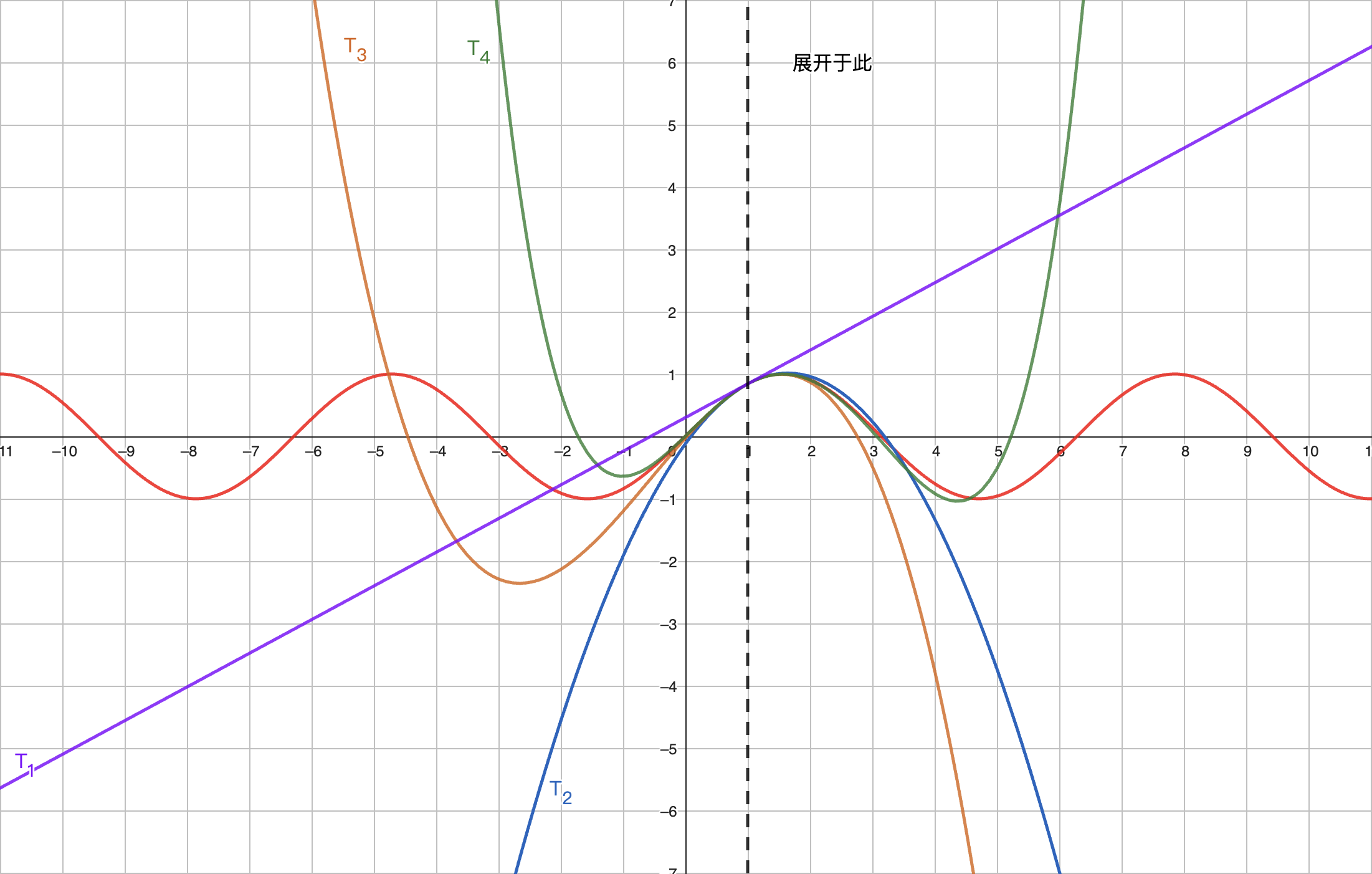
上图是对函数 $f(x)=\cos (x)$ 位于 $x_0=1$的泰勒展开。其中红线为原函数，紫线为一阶泰勒展开，蓝线为二阶泰勒展开，橙线为三阶泰勒展开，绿线为四阶泰勒展开。我们可以看到，随着泰勒展开的次数增加，展开的多项式越接近原函数。

通过上图，我们也能发现泰勒展开的两个非常有用的性质：

1. 当我们需要拟合的点 $x$ 离展开点 $x_0$ 越近，泰勒展开后的结果 $T_n(x)$ 越接近原函数的值 $f(x)$。
2. 当泰勒展开次数越高，拟合的效果越好。

我们假设 $L$ 为损失函数，我们认为 $\mathbf{w}$ 为最优权重。我们期望从 ${\mathbf{w}}_0$ 达到最优权重 $\mathbf{w}$ 。我们对损失函数 $L(\mathbf{w})$ 位于 ${\mathbf{w}}_0$ 进行一阶泰勒展开，即：

$$\begin{array}{rl}L(\mathbf{w})& \approx L({\mathbf{w}}_0)+L^{\prime }({\mathbf{w}}_0)(\mathbf{w}-{\mathbf{w}}_0)\\ & =L({\mathbf{w}}_0)+\nabla L({\mathbf{w}}_0)(\mathbf{w}-{\mathbf{w}}_0)\end{array}$$

如果我们认为更新后的权重 $\mathbf{w}$ 是 ${\mathbf{w}}_0$ 增加一个单位向量 $\mathbf{v}$ 伴有学习率 $\eta$，则可以写成

$$\begin{array}{rl}\mathbf{w}& ={\mathbf{w}}_0+\eta \mathbf{v}\end{array}$$

我们可以将上式代入到损失函数的泰勒展开中，得到：

$$\begin{array}{rl}L(\mathbf{w})& \approx L({\mathbf{w}}_0)+\nabla L({\mathbf{w}}_0)(\mathbf{w}-{\mathbf{w}}_0)\\ & =L({\mathbf{w}}_0)+\nabla L({\mathbf{w}}_0)({\mathbf{w}}_0+\eta \mathbf{v}-{\mathbf{w}}_0)\\ & =L({\mathbf{w}}_0)+\eta \nabla L({\mathbf{w}}_0{)}^T\mathbf{v}\end{array}$$

我们可以认为 $\nabla L({\mathbf{w}}_0{)}^T\mathbf{v}$ 是损失函数在 ${\mathbf{w}}_0$ 处的梯度与更新的方向 $\mathbf{v}$ 的点积。

$$\nabla L({\mathbf{w}}_0{)}^T\mathbf{v}=||\nabla L({\mathbf{w}}_0)||\cdot ||\mathbf{v}||\cdot \cos \theta$$

其中 $\theta$ 是 $\nabla L({\mathbf{w}}_0)$ 与 $\mathbf{v}$ 的夹角。

考虑单位向量 $\mathbf{v}$，其的膜长为1，即 $||\mathbf{v}||=1$。因此我们可以得到：

$$\nabla L({\mathbf{w}}_0{)}^T\mathbf{v}=||\nabla L({\mathbf{w}}_0)||\cos \theta$$

如果假设 $\nabla L({\mathbf{w}}_0)$ 的膜长不变，则其的点积越大，说明 $\theta$ 越小，也就是说我们的更新方向越接近于梯度的方向。

根据三角函数的定理，我们可以地到 $\cos \theta \in [-1,1]$，其最小值当且仅当 $\theta =\pi$ 时取到，而其最大值则为 $\theta =0$ 时取到。因此我们可以得到：

$$\nabla L({\mathbf{w}}_0{)}^T\mathbf{v}=||\nabla L({\mathbf{w}}_0)||\cos \theta \in [-||\nabla L({\mathbf{w}}_0)||,||\nabla L({\mathbf{w}}_0)||]$$

我们的目标是使 $L(\mathbf{w})$ 最小化，也就是说我们希望 $\nabla L({\mathbf{w}}_0{)}^T\mathbf{v}$ 最小化。因此我们可以得到结论：当 $\mathbf{v}$ 与 $\nabla L({\mathbf{w}}_0)$ 的夹角为180°（即 $\pi$）时，$L(\mathbf{w})$ 取得最小值。即 $\mathbf{v}$ 与 $\nabla L({\mathbf{w}}_0)$ 反向时，$L(\mathbf{w})$ 取得最小值。

考虑 $\mathbf{v}$ 为 $\nabla L({\mathbf{w}}_0)$ 的反向，且为单位向量我们可以得到：

$$\begin{array}{rl}\mathbf{v}& =-\frac{\nabla L({\mathbf{w}}_0)}{||\nabla L({\mathbf{w}}_0)||}\end{array}$$

将其代入至原函数：

$$\begin{array}{rl}\mathbf{w}& ={\mathbf{w}}_0+\eta \mathbf{v}\\ & ={\mathbf{w}}_0-\eta \frac{\nabla L({\mathbf{w}}_0)}{||\nabla L({\mathbf{w}}_0)||}\end{array}$$

考虑 $||\nabla L({\mathbf{w}}_0)||$ 是一个标量，我们可以令 $\eta =\frac{\eta }{||\nabla L({\mathbf{w}}_0)||}$，则可得：

$$\begin{array}{rl}\mathbf{w}& ={\mathbf{w}}_0-\eta \nabla L({\mathbf{w}}_0)\end{array}$$

因此我们可以证明出最终的结论：梯度下降总是能走向最深的点。

拓展：IRLS

如果将泰勒展开展开至二阶，则有

$$\begin{array}{rl}{T}_n(\mathbf{w})& =\sum _{k=0}^n\frac{L^{(k)}({\mathbf{w}}_0)}{k!}(\mathbf{w}-{\mathbf{w}}_0{)}^k\\ & =\frac{L^{(0)}({\mathbf{w}}_0)}{0!}(\mathbf{w}-{\mathbf{w}}_0{)}^0+\frac{L^{(1)}({\mathbf{w}}_0)}{1!}(\mathbf{w}-{\mathbf{w}}_0{)}^1+\frac{L^{(2)}({\mathbf{w}}_0)}{2!}(\mathbf{w}-{\mathbf{w}}_0{)}^2\\ & =L({\mathbf{w}}_0)+(\mathbf{w}-{\mathbf{w}}_0)L({\mathbf{w}}_0)+\frac{(\mathbf{w}-{\mathbf{w}}_0{)}^2}{2}{L}^{\prime \prime }({\mathbf{w}}_0)\end{array}$$

令其导数为0，我们可以得到

$$\begin{array}{rl}\frac{\partial L}{\partial \mathbf{w}}\approx \frac{\partial }{\partial w}L({\mathbf{w}}_0)+(\mathbf{w}-{\mathbf{w}}_0)L({\mathbf{w}}_0)+\frac{(\mathbf{w}-{\mathbf{w}}_0{)}^2}{2}{L}^{\prime \prime }({\mathbf{w}}_0)& =0\\ \frac{\partial }{\partial \mathbf{w}}L({\mathbf{w}}_0)+(\mathbf{w}-{\mathbf{w}}_0)L({\mathbf{w}}_0)+\frac{(\mathbf{w}-{\mathbf{w}}_0{)}^2}{2}{L}^{\prime \prime }({\mathbf{w}}_0)& =0\\ L^{\prime }({\mathbf{w}}_0)+w{L}^{\prime \prime }({\mathbf{w}}_0)-{\mathbf{w}}_0{L}^{\prime \prime }({\mathbf{w}}_0)& =0\\ L^{\prime }({\mathbf{w}}_0)+(\mathbf{w}-{\mathbf{w}}_0)L^{\prime \prime }({\mathbf{w}}_0)& =0\\ \mathbf{w}-{\mathbf{w}}_0& =-\frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}\\ \mathbf{w}& ={\mathbf{w}}_0-\frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}\\ {\mathbf{w}}^{\prime }& =\mathbf{w}-\frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}\end{array}$$

即在二阶泰勒展开中，我们认为损失函数 $L$ 的最低点可以由 ${\mathbf{w}}^{\prime }=\mathbf{w}-\frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}$ 得到。而 $\frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}$ 可以看作是 $\mathbf{w}$ 的更新方向。

因此我们可以定义新的梯度下降函数为

$$\begin{array}{rl}\mathbf{w}& =\mathbf{w}-\eta \frac{L^{\prime }({\mathbf{w}}_0)}{L^{\prime \prime }({\mathbf{w}}_0)}\\ & =\mathbf{w}-\eta \frac{\nabla L({\mathbf{w}}_0)}{H_L({\mathbf{w}}_0)}\\ & =\mathbf{w}-\eta H_L^{-1}({\mathbf{w}}_0)\nabla L({\mathbf{w}}_0)\end{array}$$

其中 $H$ 为 Hessian 矩阵，$H_L^{-1}$ 为 Hessian 矩阵的逆矩阵。

TODO

我们将新的更新公式命名为 IRLS（Iteratively Reweighted Least Squares）算法。其是一种迭代的最小二乘法，其在每次迭代中都会重新计算权重。